teori integral

Integral
1.1  Menentukan integral tak tentu dan integral tentu fungsi aljabar dan fungsi trigonometri

Oke lah kalau begitu... topik ini kayaknya sihh topik yang paling susah di kelas xii, udah gitu materi ini masuk dalam soal UN, yah paling tidak ada 5 atau 6 soal yang berbau dengan integral :D  ... gilee bangettt gak tuhh :D   au ahhh :( ... yang penting Lo itu harus banyak latihan soal-soal nihh...
pokoknya gua bakalan ngasih sama Lo semua gimana sihh cara nguasain integral dengan konsep yang simple tapi ampuh bangeettt lahh buat naklukin soal Un, biar Lo gak kuatir dengan yang namanya Ujian Nasional

yang namanya integral itu biasa anti turunan. misalnya gua punya suatu fungsi kayak gini nihh

 nah, gua kalo gua turunin maka :
                                                                   
selanjutnya gua pengen integralin 2x ...
maka :    

                      

 ke dua ruas gua integral kan, kenapa mesti ke dua ruas ??? emank gak boleh cuma di ruas kiri ajeh atau di ruas kanan doankk ??? hmmm yahh suka2 gua donkk gua yang jawab kok :p hehehe ... maaf gua bejanda .. eh salah becanda maksud nya... :D nah, kenapa mesti ke dua ruas ??? karna, ada sama dengan (=) . itu doankkk ??? iyah,,, emank kenapee ... ?? masalahh ??? :p
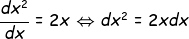
Lo harus tau apa gunanya sama dengan ....
konsep sama dengan itu apa yang Lo lakuin di ruas kiri itu juga yang Lo lakuin di ruas kanan...
 dari konsep sama dengan maka :

karna integral adalah anti turunan.
maka :
   

 nah, itu kok ada "c"  ??? itu adalah konstanta ... karna gua gak tau nilai c itu berapa yah gua buat aja "c" ...  kok bisa gitu sihh ... ??? sekarang gini, misalkan ada fungsi berikut ini :

ketiga fungsi diatas kalo gua turunin hasilnya menjadi 2x dan kalo gua integralin dengan konsep "sama dengan" maka hasilnya

kok ada "c" lagi yahh  ??? iya emang harus ada donkk ... mungkin saja nilai c itu bisa 56 trus 2 atau mungkin 234, pokoknya gak tentu bangeett lah nilai "c" itu berapa ... !!!  maka nya itu gua buat  "c" setidaknya, itu uda bisa mewakili semua nilai konstanta ... :D

karna, ketidak tentuan nilai "c" maka lahirlah yang namanya INTEGRAL TAK TENTU. masalah kapan lahir,dimana tempatnya yah itu bukan urusan gua... :D karna bukan gua yang lahirin, tapi ilmuwan pada masanya ....

sebelum gua bahas lebih jauh tentang INTEGRAL TAK TENTU, gua ngasih suatu modal buat Lo bisa naklukin soal integral. gak banyak kok, yah paling sih cuma 3 rumus doank tohhh...

nah, ini rumus pertama yang bener2 Lo harus paham dulu. di bagian ke dua gua ada nambahin bahwa U harus sama dengan dU. kenapa harus gitu ?? biar bisa di integralin aja .. :D

ada yang niat ngerjain soal di atas ??? kayaknya soal di atas ora iso di integralin tohh.... !!! yah paling enggak hasil integral nya nol. tapi kalau kek gini baru bisa...

udah tau lah yah hasil itu berapa ???!!??
nah, selanjutnya gua ngasih rumus yang ke dua dan ke tiga...

rumus yang kedua itu maksudnya jika ada suatu konstanta dalam soal integral, kita bisa keluarin konstantanya baru kita integralkan...
rumus yang ketiga jika dalam persoalan integral terdapat penjumlahan dan pengurangan, kita bisa pisahin dan kita integralkan masing-masing. contohnya berikut ini dari penggunaan rumus yang pertama sampe yang ketiga...
   

hadeh, kayaknya gua gak bahas integral tak tentu lagi nihh, yang penting pokoknya integral tak tentu itu pasti belakangnya tambah "c" .
uda ngerti gak Lo tentang integral aljabar ini, kalau Lo uda paham sekarang gua bakalan bawa ke alam integral trigonometri,yang mana ini menjadi boomerang kalau ini jadi soal ujian semester atau bahkan Ujian Nasional... kapok dehh Lo :D udah tenang ajehh Lu baca dengan baik dengan benar, karna Lu pada uda lulus SD SMP dan pastinya membaca uda lancar donkk....
gua langsung kasi ajehh dehh integral trigono, sebelumnya Lu pasti uda ngerti turunan trigono donkk...
misalnya turunan sin x itu kan cos x, maka integral cos x yah sin x
ini ada turunan trigono yang mesti Lu harus paham...
1. d sin x = cos x
2. d cos x = - sin x
3. d tan x = sec^2 x
karna integral itu anti turunan maka kita bisa membuat langkah seperti berikut...

gua harap dengan cara yang sama Lu bisa nemuin integral trigono lainya...

Integral Subtitusi, teknik ini biasanya di gunaka ketika dalam menyelesaikan soal integral terdapat sebuah turunan !!! ngerti gak Lo ???? udah Lo leat ajeh dehh berikutnya biar Lu paham :D

ketika segala daya dan sekuat semampu Lo dalam menyelesaikan soal integral, ada satu teknik lagi nihh yang gak bisa di selesaikan dengan subtitusi, dan kadang soal ini sering masuk UN lohhhh ... teknik ini bisa bikin ribet tapi bisa di simpelkan kok. caranya gimana ?? yahh Lo harus banyak2 latihan donkkk... emanknya makanan bisa langsung instan :p

Integral Parsial, gua langsung kasih rumusnya ajeh dehh... terserah kalok Lo mau nemuin yah temuin ajeh dehh,,, kalok nggak yah paling tidak Lo harus hapalin ni rumus...

selanjutnya topiki yang terakhir nii ... kalok ada tak tentu berarti pasti ada juga yang tentu 

Integral Tentu, integral tentu ini mudah saja, karna cukup di integralkan dengan cara biasa trus masukin aja batas atas dan batas bawah seperti berikut.

selesai sudah topik integral, saran gue Lo latihan2 dulu dengan konsep yang uda gua kasih, Lo bahas semua soal yang ada di buku biar Lo juga makin paham tentang integral ini yang tidak begitu sulit :D....

biasanya jika ada teori pasti ada praktek, nah karna ini matematika jadi prakteknya bahas soal...

gua pasti bakal buat pembahasan soal integral terkait SKL Un yang satu ini, pokoknya kalian harus bahas2 soal deh biar pas gua buat pembahasan nya Lo gak bingung itu dari mana ini dari mana yang pasti semua berasal dari latihan ... 

sekian dan terimakasihh...dan  jika Lo punya kritikan dan saran silakan ajehh... gua lapang dada kok :D